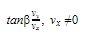ESTANDAR
PENSAMIENTO NUMÉRICO Y SISTEMA NUMÉRICO
Analizo representaciones decimales de los números reales para diferenciar entre racionales e irracionales.
PENSAMIENTO ESPACIAL Y SISTEMA GEOMETRICO
Uso argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias.
PENSAMIENTO METRICO Y SISTEMA DE MEDIDAS
Diseño estrategias para abordar situaciones de medición que requieran grados de precisión específicos.
PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRAICOS Y ANALITICOS
Analizo las relaciones y propiedades entre las expresiones algebraicas y las gráficas de funciones polinómicas y racionales y de sus derivadas
COMPONENTE
- Numérico variacional
- Geométrico métrico
INDICADOR DE DESEMPEÑO
Determino y utilizo la estructura de las funciones trigonométricas en diferentes situaciones del mundo real.
METODOLOGÍA/ SECUENCIA DIDÁCTICA
- Unidad didáctica
Gráficas de las funciones trigonométricas.
Líneas trigonométricas.
- Propósito
Apreciado estudiante el propósito de esta guía, es que confíes en tus propias capacidades para resolver problemas geométricos y así exponer tus ideas utilizando el lenguaje matemático.
- Desarrollo cognitivo instruccional
FUNCIONES TRIGONOMETRICAS Y LINEAS TRIGONOMETRICAS
Cada una de las razones que se obtienen entre las proyecciones y la longitud del segmento orientado recibe un nombre especial. Estas razones corresponden a las seis funciones trigonométricas y su valor se determina de acuerdo con el ángulo colocado en posición normal.
FUNCIÓN SENO
El seno del ángulo es la razón entre la proyección vertical del segmento orientado y su longitud.
Simbólicamente:
senβvyv
FUNCIÓN COSENO
El coseno del ángulo es la razon entre la proyección horizontal del segmento orientado y su longitud.
Simbólicamente:
FUNCIÓN TANGENTE
La tangente del ángulo es la razón entre las proyecciones vertical y horizontal del segmento orientado, siendo esta última diferente de cero.
FUNCIÓN COSECANTE
La cosecante del ángulo es la razón reciproca del seno, se define como el cociente de la longitud del segmento orientado y su proyección vertical. Esta última es diferente de cero.
FUNCIÓN SECANTE
La secante del ángulo es la razón reciproca del seno, se define como el cociente entre la longitud del segmento orientado y su proyección horizontal. Esta última es diferente de cero.
Para hallar funciones como seno, coseno, tan, por medio de la calculadora ver el siguiente video.
LINEAS TRIGONOMÉTRICAS
SENO Y COSENO.
En el triángulo ΔOPQ las funciones senΘ y cosΘ quedan determinadas directamente al medir los segmentos y’ y x’; por ello haremos nuestro análisis sobre una circunferencia de radio 1, sin perder generalidad.
Así por ejemplo, si tomamos Θ = 0°, tenemos
Ejemplo 1.
Si tenemos Θ = 0°, tenemos.
Ver el siguiente video como complemento del ejemplo
Example 2:
En un círculo de radio la unidad, identifica y mide el valor de las funciones seno, coseno, tangente, cotangente, secante y cosecante para Θ= 30°. Compara los resultados con los obtenidos con la calculadora.
Gráficamente
sen 30° = 0,5
cos 30°= 0,8
tan 30° = 0,6
cot 30°= 1,8
sec 30° = 1,2
csc 30° = 2,2
Con calculadora
sen 30° = 0,5
cos 30°= 0,86
tan 30° = 0,57
cot 30°= 1,73
sec 30° = 1,15
csc 30° = 2
- Desarrollo Metodológico.
- En un círculo de radio la unidad, identifica y mide el valor de las funciones seno, coseno, tangente para Θ= 45°. Compara los resultados con los obtenidos con la calculadora.
- En un círculo de radio la unidad, identifica y mide el valor de las funciones cotangente, secante y cosecante para Θ= 60°. Compara los resultados con los obtenidos con la calculadora.
Evaluación