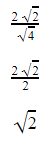ESTANDAR
PENSAMIENTO NUMÉRICO Y SISTEMA NUMÉRICO
Analizo representaciones decimales de los números reales para diferenciar entre racionales e irracionales.
PENSAMIENTO ESPACIAL Y SISTEMA GEOMETRICO
Uso argumentos geométricos para resolver y formular problemas en contextos matemáticos y en otras ciencias.
PENSAMIENTO METRICO Y SISTEMA DE MEDIDAS
Diseño estrategias para abordar situaciones de medición que requieran grados de precisión específicos.
PENSAMIENTO VARIACIONAL Y SISTEMAS ALGEBRAICOS Y ANALITICOS
Analizo las relaciones y propiedades entre las expresiones algebraicas y las gráficas de funciones polinómicas y racionales y de sus derivadas
COMPONENTE
- Numérico variacional
- Geométrico métrico
INDICADOR DE DESEMPEÑO
Identifica las propiedades de algunas funciones trigonométricas y conoce los algoritmos de las razones trigonométricas.
METODOLOGÍA/ SECUENCIA DIDÁCTICA
- Unidad didáctica
Funciones trigonométricas
- Propósito
Apreciado estudiante el propósito de esta guía, es que confíes en tus propias capacidades para resolver problemas geométricos y así exponer tus ideas utilizando el lenguaje matemático.
- Desarrollo cognitivo instruccional
RELACIONES TRIGONOMÉTRICAS PARA ÁNGULOS ESPECIALES
Valor de las relaciones trigonométricas para el ángulo de 45°
Sea un triángulo ONA, rectángulo e isósceles; OA = ON =X
Para calcular el valor de la hipotenusa del triángulo ΔONA, procedemos de la siguiente manera:
- Aplicamos el teorema de Pitágoras : h2 = x2 + x2
- Sumando términos semejantes: h2 = 2x2
- Se extrae la raíz cuadrada en los dos miembros de la igualdad: h= 2x
Valores de las relaciones trigonométricas para el ángulo el 45° son:
Valor de las relaciones trigonométricas para el ángulo de 30°
- Sea el ΔABC, equilátero cuyo lado mide x unidades.
- Trazamos AD; bisectriz del ے A.
- Como el triángulo ΔABC es equilátero, AD es altura y media respecto a la base CB.
- CB=X, luegoCD = X2
Por el teorema de Pitágoras…
x2= CD2+AD2
x2 = x22+ AD2
AD2=x2- x22
AD2=x2-x24
AD2=4x2- x2 4
AD2=3x2 4
AD2 =3x2 4
AD= 3x24
AD= 3x2
Por lo tanto los valores de las funciones trigonométricas para el ángulo de 30° son:
Valor de las relaciones trigonométricas para el ángulo de 60°
Ejemplo 1
Justifica las siguientes afirmaciones.
Solución
h2 = x22+ 32 x2
h2=x42+ 324 x2
h2=x2+3 x2 4
h2=4x2 4
h2 =4x2 4
h= 4x24
h= x
Ejemplo 2
Calcular el valor numérico de cada expresión.
Utilizando el valor de cada función, tenemos que:
Utilizamos ley de extremos y medio
Racionalizamos
- Desarrollo Metodológico
- Calcular el valor numérico de cada expresión
- Sen 45° + cos 45°
- Sen 30° + sen 60°
- Sen 30° . sen 60° - cos 30°
Evaluación